With the rise of the orbit population, particularly in LEO and GEO in recent years, the number of conjunctions continues to grow.

In GEO, satellites are assigned specific longitudes along the orbital plane, and they inevitably undergo longitudinal drift due to perturbations. East-West Station Keeping (EWSK) maneuvers are performed to counteract this issue and involve performing tangential/along-track burns in the orbital plane, amounting to a total between 2 m/s ofΔv per year up to 2.8 m/s. Similarly, inclination drift causes satellites to shift in latitude, gradually leading them beyond their designated operational control box. To counteract this, routine North-South Station Keeping (NSSK)maneuvers are necessary to uphold a stable inclination within acceptable bounds. These maneuvers can require an annual Δv expenditure ranging between 44 to 55 m/s.

The presence of these routine SK maneuvers, which might happen as often as daily, motivates the development of new capabilities that leverage these maneuvers for collision avoidance (COLA)purposes. The aim is to avoid the requirement of additional maneuvers just for collision avoidance.

OKAPI:Aether – Optimized Collision Avoidance Maneuvers with Station-Keeping Constraints

In this report, a new feature for OKAPI:Aether is introduced, that extends the collision avoidance maneuver generation capabilities with consideration of station-keeping constraints for satellites in the GEO regime. Numerical simulations were conducted for validation and to show the effectiveness of the new feature in generating maneuvers that satisfy collision avoidance and station-keeping constraints simultaneously.  

For collision avoidance, current practices emphasize using collision probability and miss distance as key constraints, which are adopted in this work. Satellite platform constraints, such as limited propellant, also need consideration as they limit the number of maneuvers a satellite can perform. The goal is to reduce operational costs by minimizing the Δv required for maneuvers that meet all constraints.

Two use cases reflect real-world relevance, helping to implement features and address user needs. Each use case corresponds to an objective function, control variable, and constraints. Across all use cases, the cost function is total Δv, the control variable is the maneuvered Δv, and the constraints are either miss distance or collision probability for collision avoidance and Control-Box bounds or target inclination for station keeping.

GEO Maneuver Optimization: Control-Box and Miss Distance

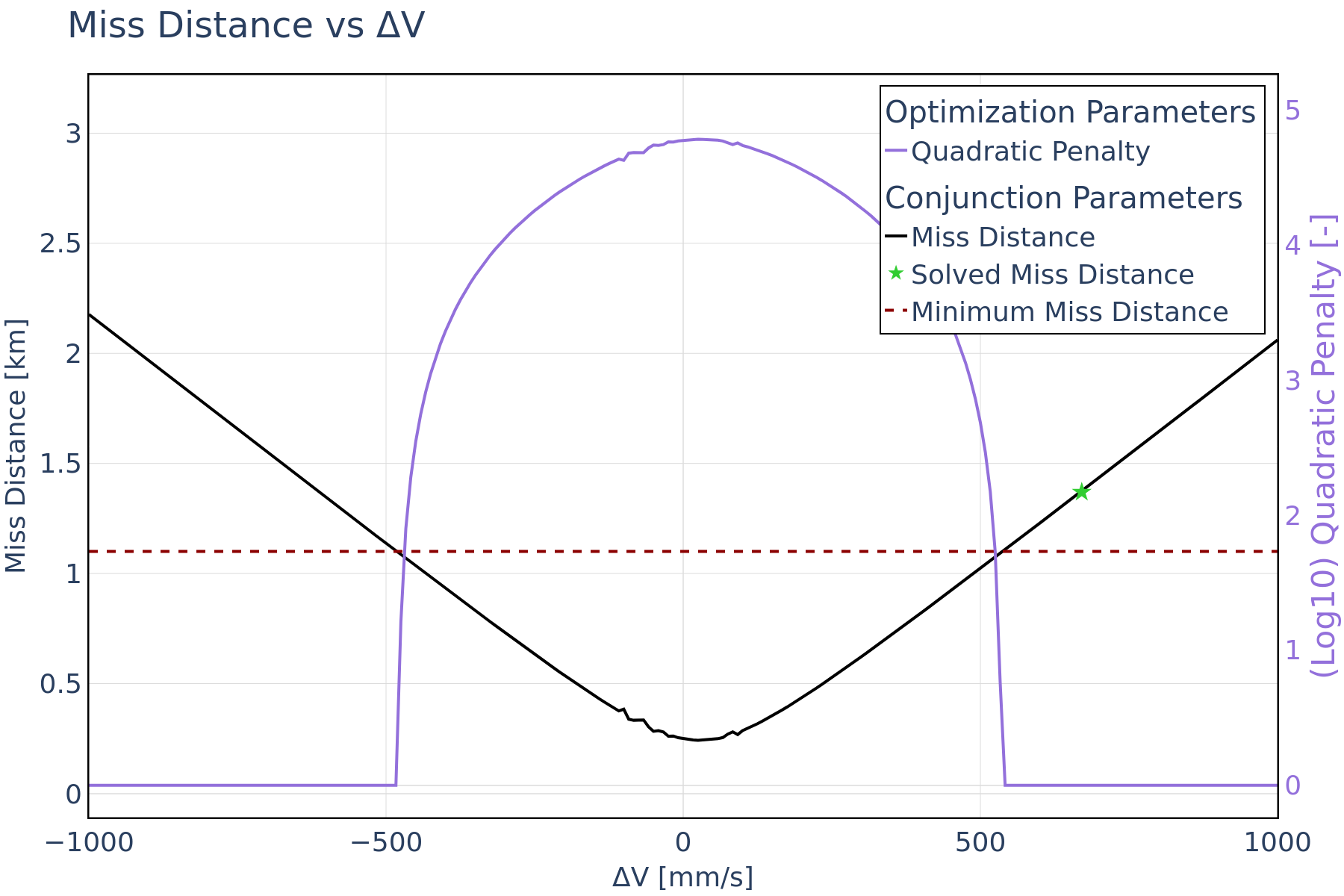
The objective is the integration of the station-keeping constraints specific to the GEO domain into the optimization framework. In this case, a control-box inequality constraint is implemented to satisfy the needs defined in use case 1. All key parameters are detailed in the tables below. The GEO control box is an object-centered box defined by maximum deviation limits in the RTN frame. A CAM should be performed which does not exceed the defined limits. The aggregated cost function includes the nominal cost, the minimum miss distance, maximum radial, along-track, and cross-track deviation constraints. In this unconstrained optimization problem, the min. miss distance and the deviation constraints act as penalty functions.

The optimization results are depicted in the plot in Figure 1. The black line represents the aggregated cost function, which shows how the overall cost, including all constraints, changes with respect to Δv.The green star marks the computed optimal Δv where the maneuver cost is at its lowest while satisfying all constraints. The aggregated cost function presents a pronounced peak and valley. The peak indicates a high-cost region, signifying poor maneuver outcomes from a miss-distance standpoint. This shows that the cost function aggregation successfully considered the miss distance constraints. The valley on the other hand represents a low-cost region. The colored lines in the plot represent the convergence performance from different initial conditions. The pink line shows the iteration trajectory starting from an initial Δv = 0 in the prograde direction, while the purple line indicates the iteration trajectory starting from the maximum Δv value in the prograde direction. As can be observed, the framework converges quickly towards the optimal solution for both initial conditions.  

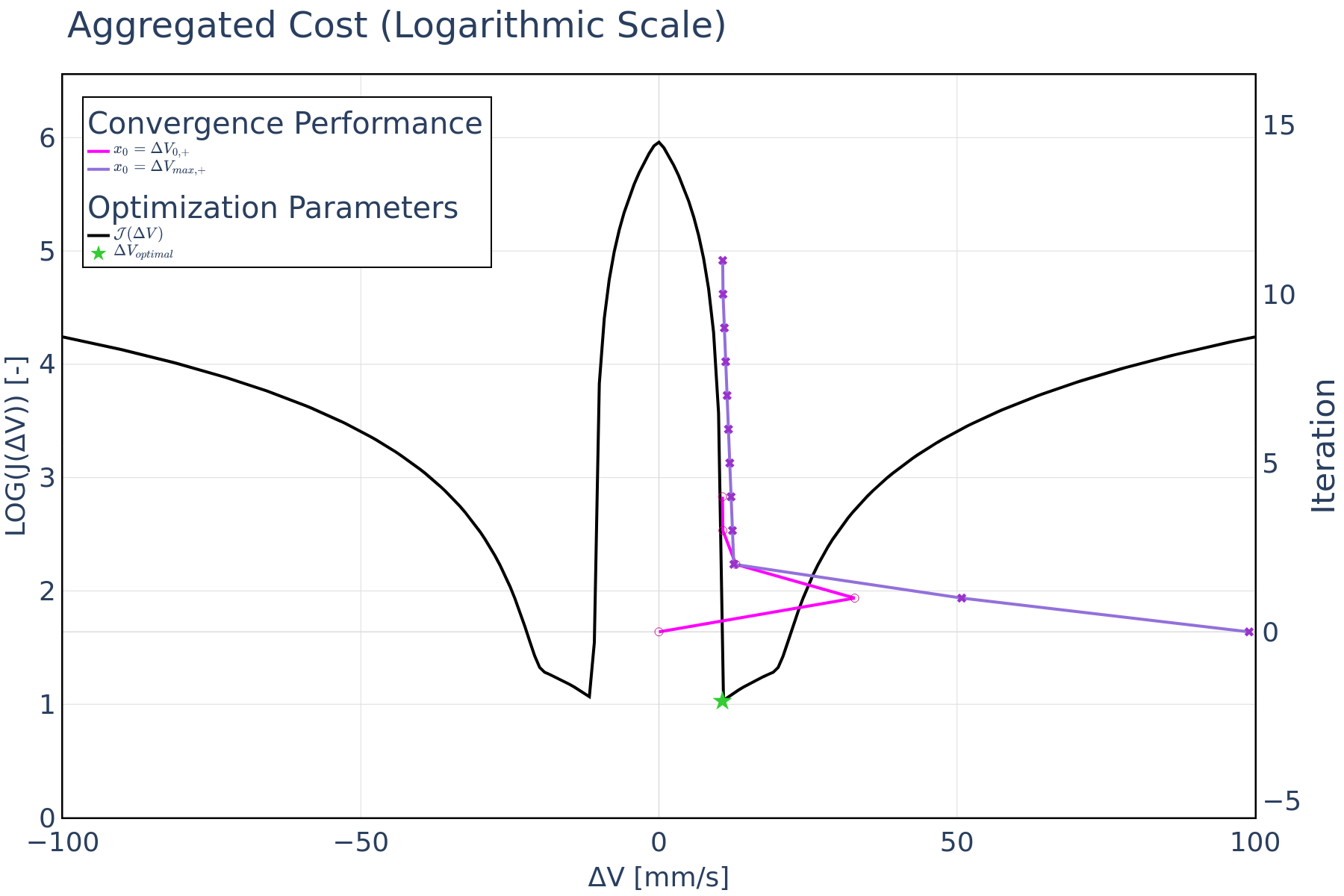
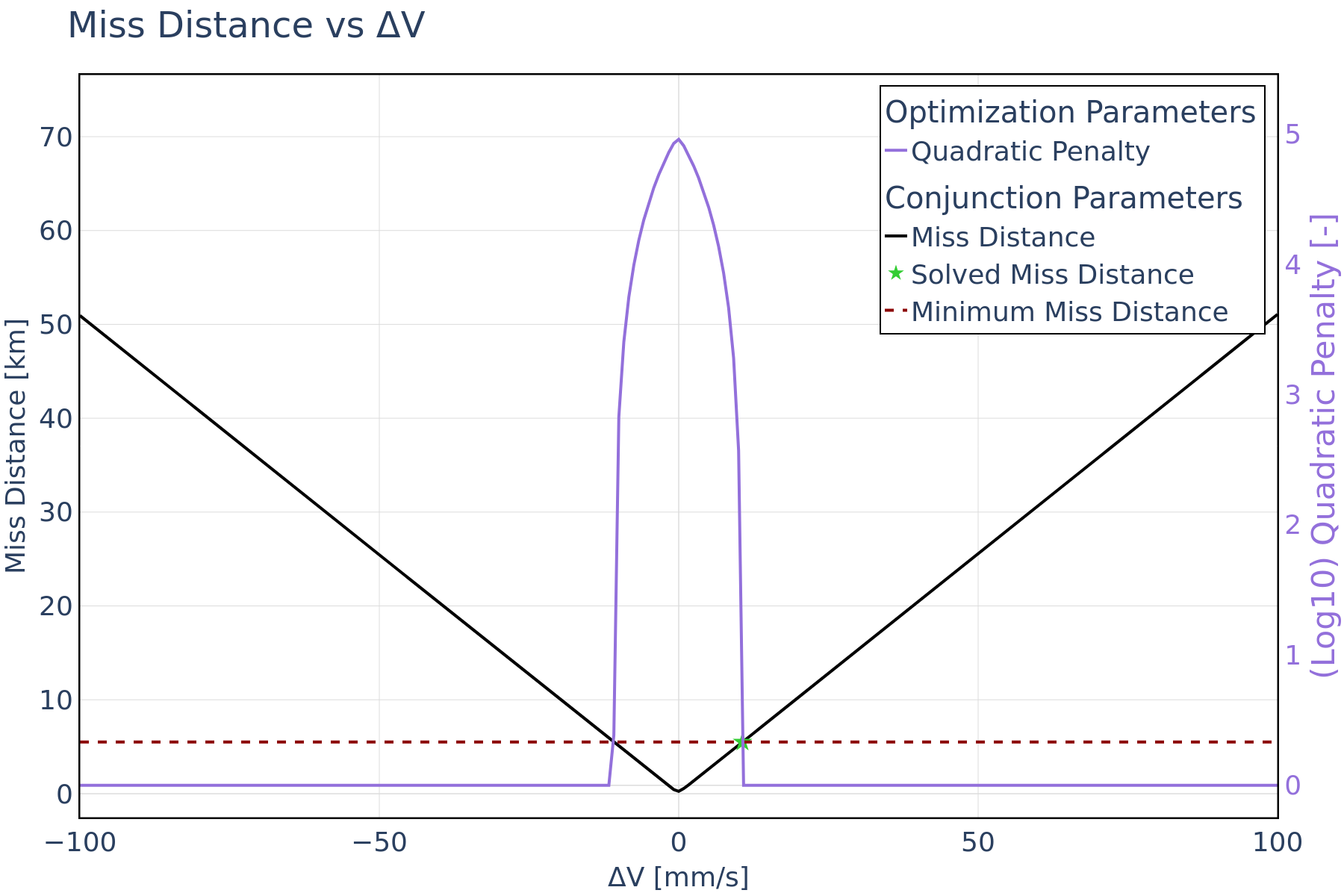
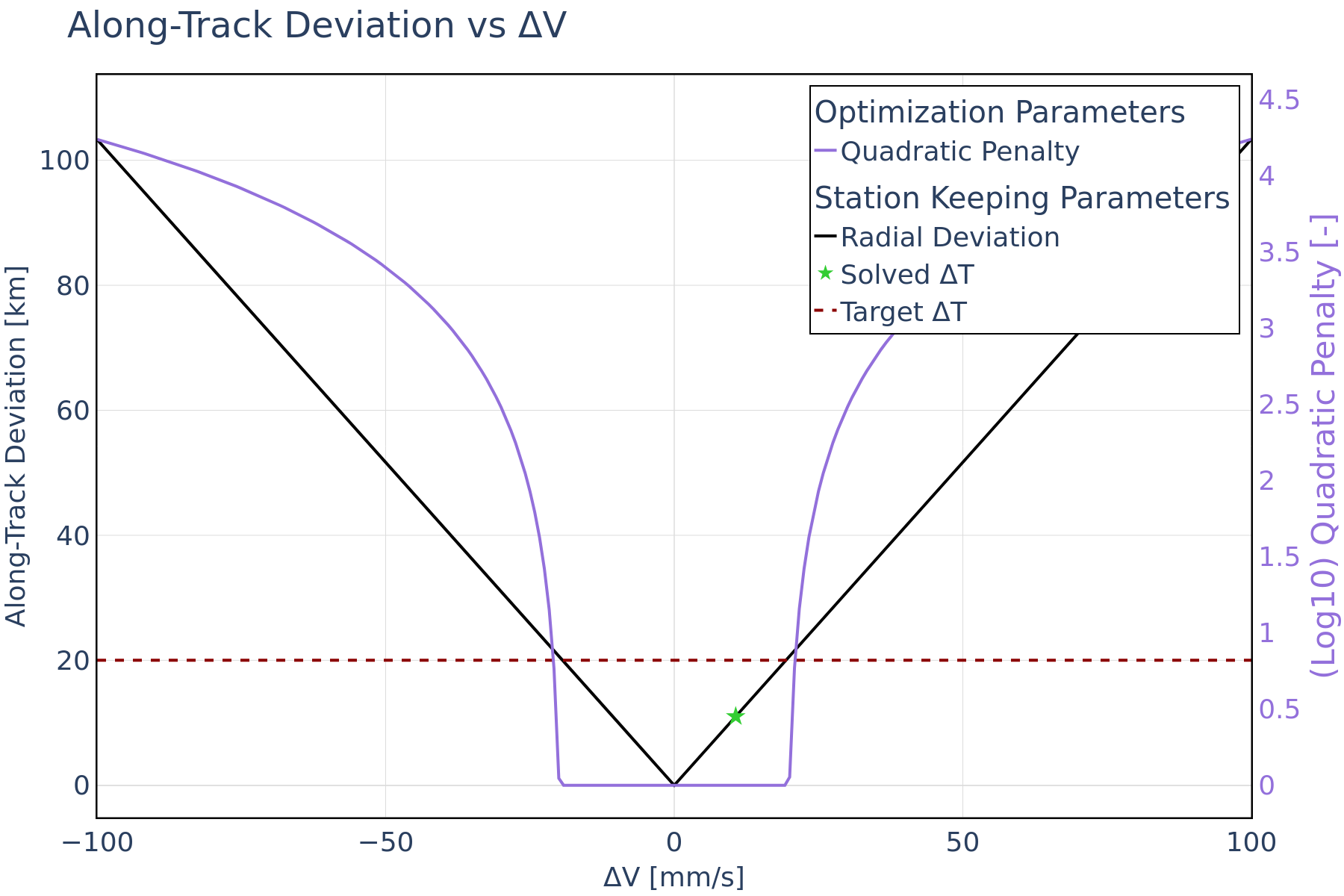
Figure 2 shows the miss distance constraint and the superposed miss distance penalty function, the along-track deviation is displayed in Figure 3 – as part of the control-box constraint - with its corresponding penalty function. Because the maneuver in this use case is solely performed in the along-track direction, its effect on radial and cross-track deviation is negligible. Therefore, only the along-track deviation is shown here. For this use case, the control-box constraint is satisfied since the optimal solution remains below the maximum along-track deviation threshold.

GEO Maneuver Optimization: Target Inclination and Miss Distance

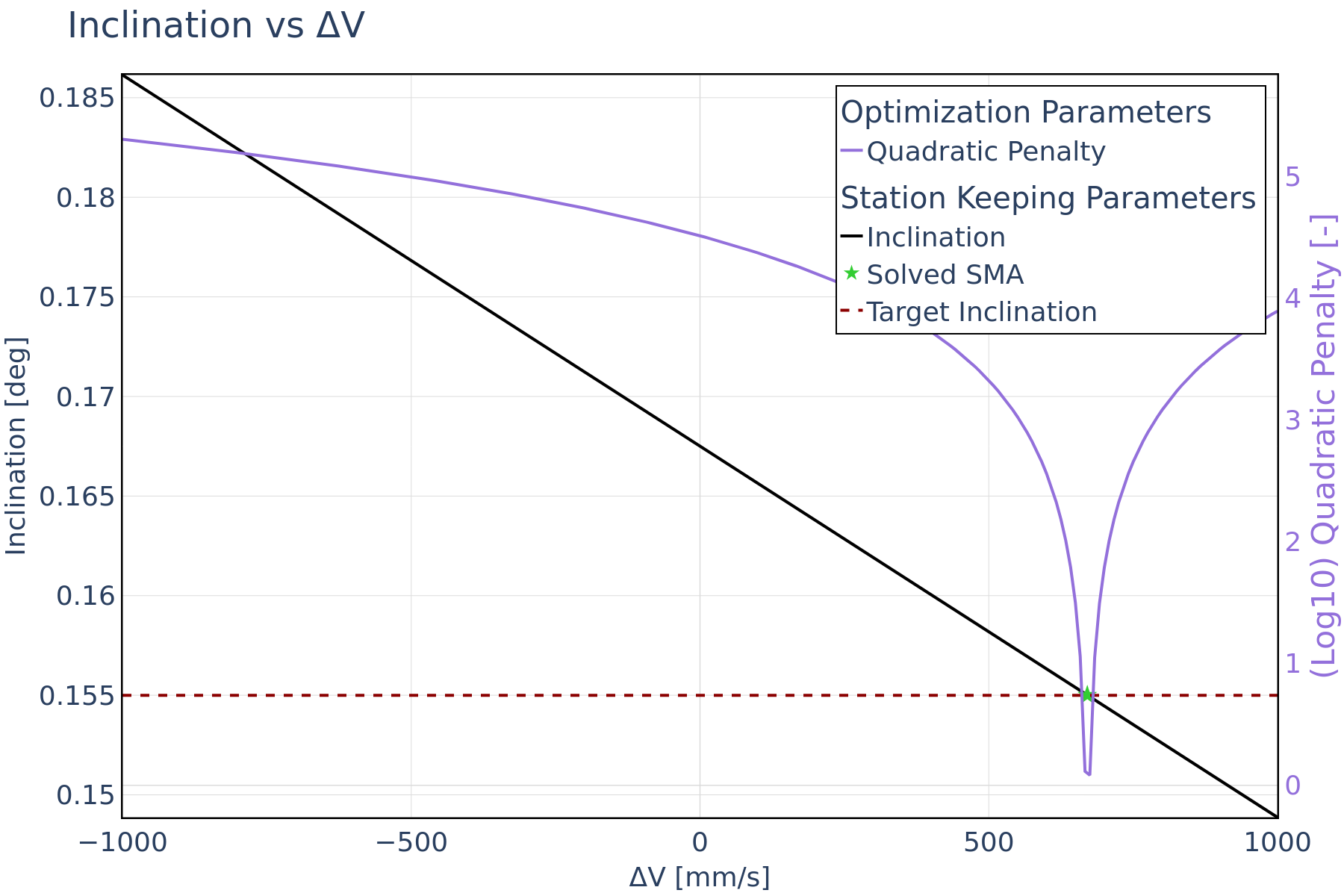
In this use case, the inclination equality constraint is incorporated to add the NSSK functionality into the optimization framework. It is important to note that NSSK involves changing the orbital plane of a satellite. This requires inclination change maneuvers, which can only be achieved with an out-of-plane component in the maneuver direction. For maximum efficacy and to attain very low inclinations, the maneuver must be executed at one of the nodal points of an orbit.

For this use case, the aggregated cost function includes the Δv, the min. miss distance inequality constraint, and the target inclination equality constraint. In this scenario, the optimization framework aims to minimize Δv while maintaining a minimum miss distance and reaching a specified target inclination. The magnitudes of the required Δv’s are notably higher compared to previous cases. This increase is attributed to the inclusion of plane change constraint, executed either in the normal or anti-normal direction, which generally requires larger Δv. The direction of the maneuver is set to either normal or anti-normal based on whether the target inclination exceeds the initial inclination values.

Additionally, the timing of the maneuver epoch holds significance, since it must coincide with either the ascending or descending node, as previously detailed. This ensures proper alignment with the desired inclination adjustment. Both the Δv = 0 initial guess approach and the maximum Δv schemes rapidly reach the global minimum with a relatively low iteration count.

‍

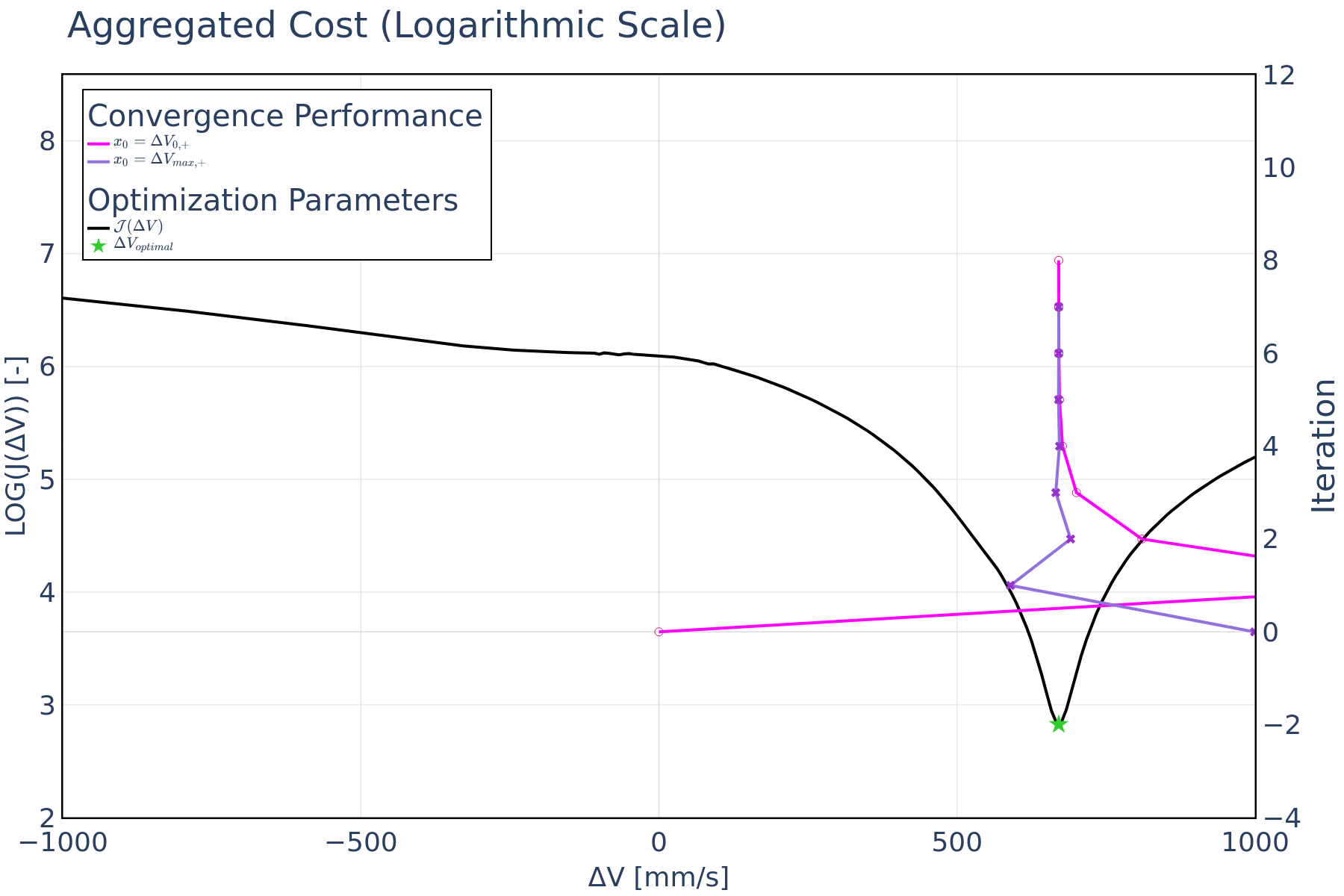
Along-track maneuvers are usually the less costly because they change in the orbital which leads to an increase of period along-track separation with each revolution. In contrast, cross-track maneuvers do not offer this advantage, hence, they are less effective for collision avoidance. However, due to the relatively large Δv involved in NSSK maneuvers, these can suffice for effective collision risk mitigation.  Unlike the previous use case, the miss distance progression in Figure 4 exhibits a slight variation. This is primarily due to the specific demands of inclination change maneuvers, which require more Δv to execute the inclination change. As depicted in Figure 5, the optimization framework comfortably meets the miss distance constraint. The inclination with its corresponding penalty function is illustrated in Figure 6.

Real-World Impact and Future Directions

Through a series of use cases, the COLA maneuver optimization framework demonstrated its ability to minimize maneuver costs while meeting a variety of constraints. The approach achieved consistent and rapid convergence for the use cases, where control-box station-keeping and target inclination constraints were considered in the COLA optimization process.

Although the presented use cases focus on two GEO-specific scenarios, the framework can be applied to any regime, and a wide range of constraints is  considered for station-keeping purposes.

In conclusion, the framework enables a useful feature for satellite operators to effectively mitigate collision risk by repurposing station-keeping maneuvers. This reduces their operational costs and increases the satellite's lifetime. The framework is poised to drive tangible improvements to satellite mission planning and execution, ensuring better performance and adaptability in real-world space environments.

Learn more about OKAPI:Aether and its latest features. Schedule a call with our team today.